Annealed Multiple Choice Learning: Overcoming limitations of Winner-takes-all with annealing
Résumé
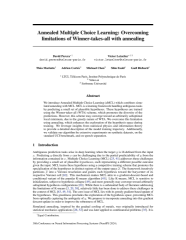
We introduce Annealed Multiple Choice Learning (aMCL) which combines simulated annealing with MCL. MCL is a learning framework handling ambiguous tasks by predicting a small set of plausible hypotheses. These hypotheses are trained using the Winner-takes-all (WTA) scheme, which promotes the diversity of the predictions. However, this scheme may converge toward an arbitrarily suboptimal local minimum, due to the greedy nature of WTA. We overcome this limitation using annealing, which enhances the exploration of the hypothesis space during training. We leverage insights from statistical physics and information theory to provide a detailed description of the model training trajectory. Additionally, we validate our algorithm by extensive experiments on synthetic datasets, on the standard UCI benchmark, and on speech separation.
Fichier principal
 main.pdf (7.17 Mo)
Télécharger le fichier
Figure1_synthetic.pdf (1.11 Mo)
Télécharger le fichier
Figure2_rate.pdf (128.77 Ko)
Télécharger le fichier
Figure3_distortion.pdf (129.33 Ko)
Télécharger le fichier
Figure4_transition.png (768.59 Ko)
Télécharger le fichier
Figure5_relaxed.png (6.14 Mo)
Télécharger le fichier
Figure6_perf.png (482.81 Ko)
Télécharger le fichier
Figure7_nhyp_amcl.pdf (32.47 Ko)
Télécharger le fichier
Figure7_nhyp_mcl.pdf (32.46 Ko)
Télécharger le fichier
Figure8_transition.pdf (167.52 Ko)
Télécharger le fichier
main.pdf (7.17 Mo)
Télécharger le fichier
Figure1_synthetic.pdf (1.11 Mo)
Télécharger le fichier
Figure2_rate.pdf (128.77 Ko)
Télécharger le fichier
Figure3_distortion.pdf (129.33 Ko)
Télécharger le fichier
Figure4_transition.png (768.59 Ko)
Télécharger le fichier
Figure5_relaxed.png (6.14 Mo)
Télécharger le fichier
Figure6_perf.png (482.81 Ko)
Télécharger le fichier
Figure7_nhyp_amcl.pdf (32.47 Ko)
Télécharger le fichier
Figure7_nhyp_mcl.pdf (32.46 Ko)
Télécharger le fichier
Figure8_transition.pdf (167.52 Ko)
Télécharger le fichier
| Origine | Fichiers produits par l'(les) auteur(s) |
|---|
| Origine | Fichiers produits par l'(les) auteur(s) |
|---|



